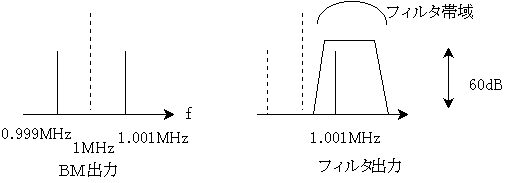１.SSBへの応用

最近DSPによるいろいろなアプリケーションが発表されているが、SSBをディジタルによって発生する方法に興味深いものがあるので、それについてのべる。
なお用語の定義、表現について、若干厳密を欠く場合があるかもしれないが、素人無線ということでご容赦頂きたい。

1.1 アナログによるSSBの発生の方法

現在までよく使用されてきた方法に次の２つがある。

a) Filter　type
b) PSN　type

これらの方式については一般的なので、ここでは詳しくは述べない。しかし、a)については

1)　シェープファクタのよいフイルタが必要
2)　群遅延特性が位相歪に影響を与える
3)　1,2は相反する特性であること

などの問題がある。

また、b)では

1)　特性のよいAF-PSNが作りずらい

ということにある。

1.2 ディジタルによるSSBの発生方法

ディジタルによってSSBを発生するためのブロック図はつぎのようになる。

MIC　-->　A/D　-->　DSP　-->　D/A　-->　SSB　OUT
A/D : Analog to Digital converter
DSP : Digital Signal Processor
D/A : Digital to Analog converter

このブロックで、Filter　type，PSN　type　のどちらの方法でも実現可能である。
PSN　typeでは、Kenwoodの　TS950　で実現されていて、回路の規模、ROMの容量、性能など現実的である。
但し、自作するとなるとヒルベルト変換(AF-PSNをデジタルで作る方法)がちょっととっつきにくいため、なかなかシミュレーションしずらい。
自作としてはわざわざ難しいＰＳＮタイプを作る必要はないので、デジタルフィルタの特徴である群遅延特性の良い（理論的にはゼロ）フィルタタイプを実現することを考える。

２.ふたたび Filter　type (アナログ)のSSB-Generatorについて

MIC　-->　BM　-->　FILTER　-->　OUT

このブロック図で、いったいBMとFilterとはどの様な動作をしているのかを考えてみる。
BMで作られたDSBの信号は、Filterによって一方のサイドバンド、例えばUSBが欲しい場合はFilterによってLSBが削られてSSBになるわけであるが、この時LSBはFilterの減衰帯域にあり,USBは通過帯域にあるように周波数が選択される。
例えばキャリアが１ＭＨｚで、変調波が１ＫＨｚのときDSB変調された信号は１．００１ＭＨｚと０．９９９ＭＨｚにスペクトラムが発生する。
ここで、USB用のフィルタを通すと、１．００１ＭＨｚは減衰せずに通過し０．９９９ＭＨｚはたとえば６０ｄＢ減衰する。これは周波数スペクトラムで見ればちょうどフィルタの帯域内の周波数の信号に対しては”係数　１”をかけ算し、それ以外の周波数（ここでは０．９９９ＭＨｚを含む帯域内のすべての周波数）に”係数　０．００１”をかけ算したのと同じ結果となる。
（実際のアナログフィルタはかけ算を行っているわけではない。目的以外の信号は反射して入力に戻してしまうように動作する。）
キャリアはBMで抑圧されているので、USBが取り出せる。
また、BMは信号とキャリアをかけ算するように動作する、単なる掛け算器である。

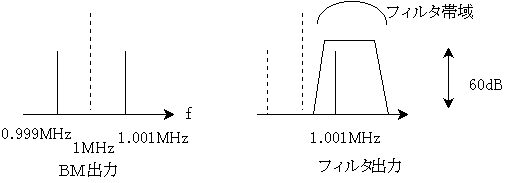
３.デジタルでの信号の扱い（DSPの動作）

3.1 サンプリング

アナログ信号をデジタル信号に変換するためには、アナログ信号に対して”サンプリング”という操作を行う。
”サンプリング”とは、もとの信号（ここではAFの信号）をサンプリングしたい周期でその電圧値を固定することであり、その方法は電圧値を数A/D変換器でデジタル信号にすることである。
１ＫＨｚのAF信号を例えば４ＭＨｚでサンプリングしA/D変換すると、０．２５usごとに切り取った１ＫＨｚの電圧値がデジタルの数値として得ることができる。

3.2 BM

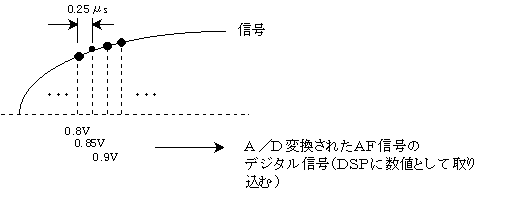
Ａ／Ｄされた信号はバランスド・モジュレータ（BM）でＤＳＢにされる。これをDSPで実現するためには、BMとは(AF)信号とキャリアとの”かけ算”であることを考えれば、”(AF)信号のA/D変換したデジタル信号（信号ということにする）　とキャリアをA/D変換したデジタル信号（キャリアという）　をかけ算すればよい。”ということになる。
但し、信号とキャリアは　”同じ周波数でサンプリングしたデジタル信号でなければいけない。”また、キャリアに関しては特にサイン波である必要はないので、取扱の容易な矩形波でよい。
ＤＳＰでは、前の例で考えると、１ＭＨｚ（キャリア、矩形波）を４ＭＨｚでサンプリングすることになるから、結果は

１，１，−１，−１，１，１，−１，−１・・・・

となる。
これを信号とかけ算するのだから、この場合、信号の符号を２つおきに２個ずつ反転することと同じになり、そのようにプログラム処理すればよい。
キャリアとサンプリングが整数倍であるときにはこのように簡単であるが、そうでない時には、キャリアを実際にサンプリング周波数でサンプリングしてキャリアデータを作り、それと信号をかけ算しなくてはならない。

3.3 フィルタ

前述のように、フィルタを通すことは

”周波数領域で、信号とフィルタの減衰特性をかけ算すればよい”

ということがわかった。
デジタルではいったいどのようにすればよいのか？
そのためには次のような定理がある。

”周波数領域のかけ算は、時間領域のたたみこみ　という操作によって実現できる。”

つまり、時間領域での信号（信号そのもの）と、時間領域のフィルタの形状を表す係数列（何だか知らないが周波数領域のフィルタの減衰特性をある方法によって時間領域に変換した係数・・実際にはある意味をもった数列）　とに　”たたみこみ”　という操作を行え！ということである。

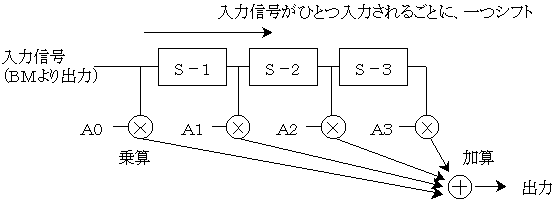
たたみこみとは

★サンプリングされた入力信号の値を　Ｓ，（Ｓ−１），（Ｓ−２），（Ｓ−３）
★フィルタの係数列を　　　　　　　　Ａ０，　　Ａ１，　　　Ａ２，　　　Ａ３
としたときに
サンプリングされた入力信号がひとつ入ってくる度に、
　　　　　　そのデータＳと係数Ａ０をかけ算する。
　　　　　　一つ前の信号（Ｓ−１）と係数Ａ１をかけ算する。
　　　　　　二つ前の信号（Ｓ−２）と係数Ａ２をかけ算する。
　　　　　　三つ前の信号（Ｓ−３）と係数Ａ３をかけ算する。
　　　　　　その結果を全部加えて、出力Ｄとする。
この操作をひとつのデータが入力されるごとに繰り返していくと、出力は信号をフィルタを通した場合と同じことになる。

これをＦＩＲフィルタ(Finite　Impulse　Response　フィルタ)という。
群遅延歪みが０である、計算回数が多い、入出力のディレイが大きいなどの特徴がある。 この中で群遅延歪については、アナログフィルタでは実現できない、デジタルだけの特徴である。
ＤＳＰは積和演算を得意とするので、このような処理はＤＳＰ向きである。
従ってＤＳＰでは、ほかの条件が満足する限りこの方法を取るのが良いと思える。
この出力をＤ／Ａ変換器でアナログ電圧に変換すると、ＳＳＢの信号になる。
係数Ａがどのくらいの個数が必要になるかというと、フィルタの性能による。
今回試作したものは、シェープファクタ（６０ｄＢ／６ｄＢ）を１．２とした場合、１５１個の係数となった。したがってサンプリングされたデータがひとつ入力されるたびに、１５１回の積和を行い、一つのデータを出力することになる。
シェープファクタと係数の算出はとても複雑なのでここでは述べない。
このほかＩＩＲフィルタ（Ｉｎｆｉｎｉｔｅ　Impulse　Response　フィルタ）もある。
どのようにＤＳＰが動作しているかを述べてきた。
さて実際にはどうするの？ということになるが、これは次回にいたします。